Multivariate normal distribution

Recall

Recall the univariate case: Univariate normal distribution.

$$f(x|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{1}{2}\frac{(x-\mu {)}^2}{{\sigma }^2}\right)$$

Now here, $\sqrt{2\pi {\sigma }^2}$ and $\frac{(x-\mu {)}^2}{{\sigma }^2}$ both should result in scalar.

Note that $\frac{(x-\mu {)}^2}{{\sigma }^2}=(x-\mu ){\sigma }^{-2}(x-\mu )$ is the square distance between $x$ and $\mu$. See Statistical Distance.

a Let us generalize this to a random vector of size $p\times 1$:

$$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$$

Here, ${\Sigma }^{-1}$ is called Precision matrix.

Then for any random vector $X$, p-dimensional multivariate normal density is:

$$f(X|\mu ,\Sigma )=\frac{1}{(2\pi {)}^{p/2}|\Sigma {|}^{1/2}}\exp \left(-\frac{1}{2}(X-\mu {)}^T{\Sigma }^{-1}(X-\mu )\right)$$

and it is denoted by

$$X\sim N_p(\mu ,\Sigma )$$

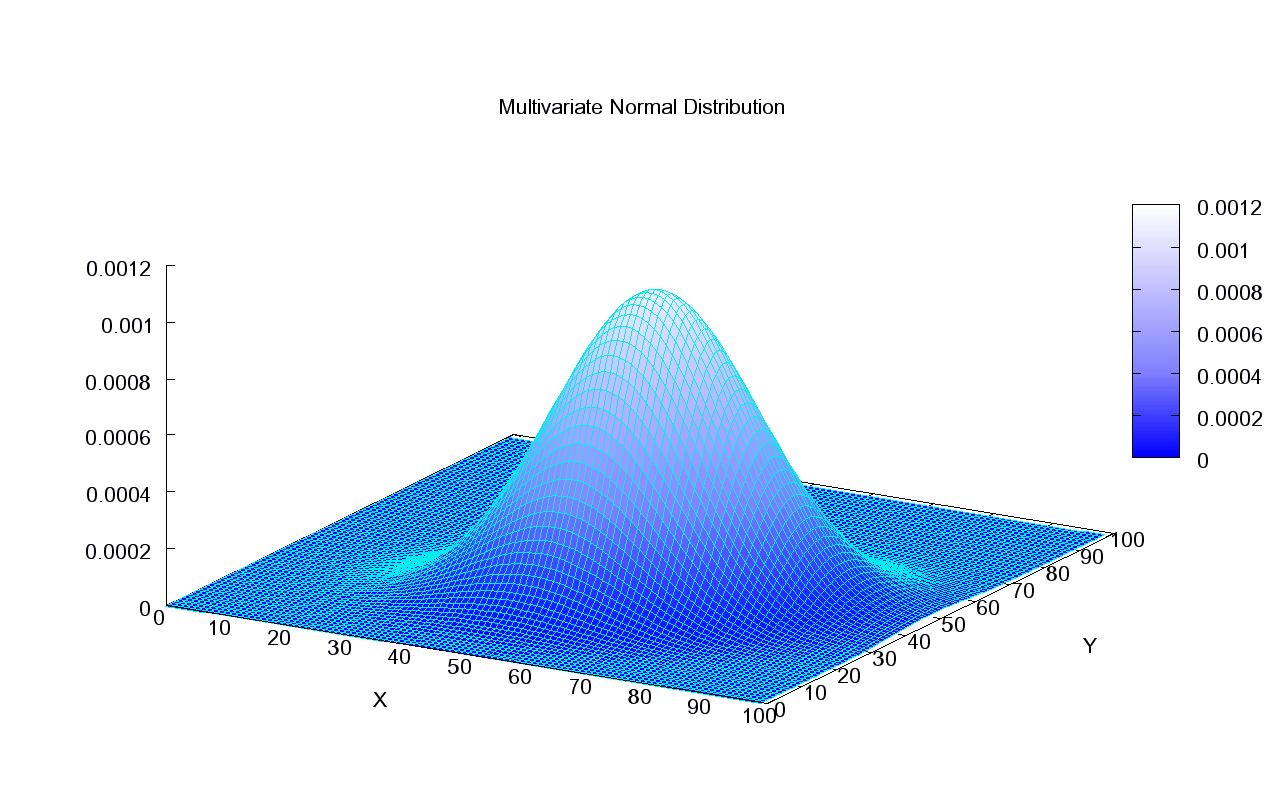
One can show a $N_2$ distribution visually as following:

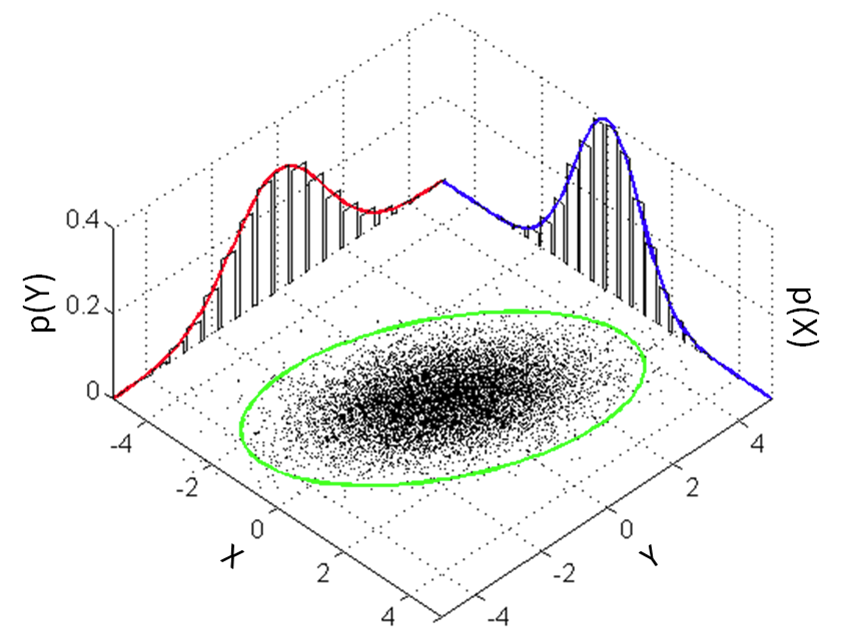
Bivariate Normal Density

First check ${\Sigma }^{-1}$:

$${\Sigma }^{-1}=\frac{1}{\det \Sigma }adj(\Sigma )$$

where $adj$ is the Adjugate Matrix.

Recall that ${\rho }_{12}=\frac{{\sigma }_{12}}{\sqrt{{\sigma }_{11}{\sigma }_{22}}}$. Then,

$$\begin{array}{rl}{\Sigma }^{-1}& =\frac{1}{{\sigma }_{11}{\sigma }_{22}-{\sigma }_{12}^2}\left[\begin{array}{cc}{\sigma }_{22}& -{\sigma }_{12}\\ -{\sigma }_{21}& {\sigma }_{11}\end{array}\right]\\ & =\frac{1}{{\sigma }_{11}{\sigma }_{22}(1-{\rho }_{12}^2)}\left[\begin{array}{cc}{\sigma }_{22}& -{\rho }_{12}\sqrt{{\sigma }_{11}{\sigma }_{22}}\\ -{\rho }_{21}\sqrt{{\sigma }_{11}{\sigma }_{22}}& {\sigma }_{11}\end{array}\right]\\ & =\frac{1}{1-{\rho }_{12}^2}\left[\begin{array}{cc}\frac{1}{{\sigma }_{11}}& -\frac{{\rho }_{12}}{\sqrt{{\sigma }_{11}{\sigma }_{22}}}\\ -\frac{{\rho }_{12}}{\sqrt{{\sigma }_{11}{\sigma }_{22}}}& \frac{1}{{\sigma }_{22}}\end{array}\right]\end{array}$$

Then,

$$\begin{array}{rl}(X-\mu {)}^T{\Sigma }^{-1}(X-\mu )& =\left[\begin{array}{cc}{x}_1-{\mu }_1& x_2-{\mu }_2\end{array}\right]{\Sigma }^{-1}\left[\begin{array}{c}{x}_1-{\mu }_1\\ x_2-{\mu }_2\end{array}\right]\\ & =\frac{1}{1-{\rho }_{12}^2}\left[{\left(\frac{x_1-{\mu }_1}{\sqrt{{\sigma }_{11}}}\right)}^2+{\left(\frac{x_2-{\mu }_2}{\sqrt{{\sigma }_{22}}}\right)}^2-2{\rho }_{12}\left(\frac{x_1-u_1}{\sqrt{{\sigma }_{11}}}\right)\left(\frac{x_2-u_2}{\sqrt{{\sigma }_{22}}}\right)\right]\end{array}$$

So the general form is

$$f_X(X)=\frac{\exp \left[\frac{-1}{2(1-{\rho }_{12}^2)}\left[{\left(\frac{x_1-{\mu }_1}{\sqrt{{\sigma }_{11}}}\right)}^2+{\left(\frac{x_2-{\mu }_2}{\sqrt{{\sigma }_{22}}}\right)}^2-2{\rho }_{12}\left(\frac{x_1-u_1}{\sqrt{{\sigma }_{11}}}\right)\left(\frac{x_2-u_2}{\sqrt{{\sigma }_{22}}}\right)\right]\right]}{2\pi \sqrt{{\sigma }_{11}{\sigma }_{22}(1-{\rho }_{12}^2)}}$$

One can memorize that by

$$f_X(X)=\frac{\left(\exp \left[-\frac{1}{2(1-{\text{correlation}}^2)}\left[d(x_1{)}^2+d(x_2{)}^2-2\text{ correlation }d(x_1)d(x_2)\right]\right]\right)}{2\pi \sqrt{{\sigma }_{11}{\sigma }_{22}(1-{\text{correlation}}^2)}}$$

where $d()$ is Statistical Distance.

If ${\rho }_{12}=0$ then,

$$\begin{array}{rl}f(x_1,x_2)& =\frac{\left(\exp \left\{-\frac{1}{2}(d(x_1{)}^2+d(x_2{)}^2)\right\}\right)}{2\pi \sqrt{{\sigma }_{11}{\sigma }_{22}}}\\ & =\frac{1}{\sqrt{2\pi {\sigma }_{11}}}\exp \left(-\frac{1}{2}d(x_1{)}^2\right)\frac{1}{\sqrt{2\pi {\sigma }_{22}}}\exp \left(-\frac{1}{2}d(x_2{)}^2\right)\\ & =f(x_1)f(x_2)\end{array}$$

where $X_1\sim N(u_1,{\sigma }_{11})$ and $X_2\sim N(u_2,{\sigma }_{22})$ and they are independent.